Inhaltsangabe Verbergen

3 Wie beweist man eine Ungleichung mit Hilfe der vollständigen Induktion?

4 Warum fügen wir die Voraussetzung ein?

Was du lernen wirst

In diesem Beitrag lernst du, wie man eine Ungleichung mit Hilfe der Vollständigen Induktion beweisen kann. Dafür solltest du am besten schon wissen wie ein Induktionsbeweis abläuft. Falls du es noch nicht weißt, kannst du dir diesen Beitrag durchlesen:

Was du mit damit anfangen kannst

Wenn du verstehst, wie man eine Ungleichung mit Hilfe der vollständigen Induktion beweist, dann kannst du eine gute Note schreiben und es für den Rest deines Lebens wieder vergessen.

Klausurtipp

Es gibt bei allen Arten von Induktionsbeweisen(Ungleichungen, Teilbarkeit, Summenformen) ein Merkmal, was es unterscheidet. Auf dieses Merkmal weise ich immer in den Beiträgen hin! (siehe unten)

Wie beweist man eine Ungleichung mit Hilfe der vollständigen Induktion?

Ich gehe davon aus, dass dir die Schritte der vollständigen Induktion bereits bekannt sind. Falls nicht, hier hast du eine kleine Zusammenfassung des Ablaufs:

Induktionsanfang(Wir beweisen, dass die Aussage für die kleinste Zahl wahr ist.)
Induktionsschritt(Wir beweisen, dass die Aussage auch für alle Zahlen über dem Startwert gilt.)
1. Induktionsvoraussetzung formulieren(Wir schreiben aus, dass unsere Annahme für ein 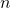$n$ gültig ist.)
2. Induktionsbehauptung formulieren(Wir formulieren unser Ziel, und zwar, dass wenn es für ein beliebiges 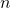$n$ gilt, es auch für das darauf folgende 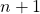$n+1$ gilt.)
3. Beweis des Induktionsschrittes(Unter Verwendung der Annahme formen wir solange um, bis wir die Form der Behauptung erreichen.)

Ich werde das Konzept an einem einfachen Beispiel erklären:

Beweise mit Hilfe der vollständigen Induktion, dass folgende Aussage gilt.

$A(n): n^2 >2n + 1 \hspace{0.5cm} \forall n \geq 3$

Kleine Randinformation: In dem Beweis, würdest du höchstens Abkürzungen wie (IA) = Induktionsanfang, (IV) = Induktionsvoraussetzung, (IB) = Induktionsbehauptung, (IS) = Induktionsschritt verwenden. Text gehört ebenfalls zur Beweisführung dazu.

(IA)

$A(3)$ : $3^2 >2 * 3 + 1$
$\Leftrightarrow 9 > 7$

(IV)

Die Aussage $A(n)$ gilt für ein beliebiges, aber festes $n$ .
$A(n): n^2 >2n + 1 \hspace{0.5cm} \forall n \geq 3$

(IB)

Wenn $A(n)$ gilt, dann gilt auch $A(n+1)$ .
$A(n+1): (n+1)^2 >2(n+1) + 1$

(IS)

$(n+1)^2$
$= n^2 + 2n + 1$
$> 2n + 1 + 2n + 1$
$> 2n + 3$

Quod erat demonstrandum.

(IA)

Da es nur für alle Zahlen $\geq 3$ gelten soll, setzen wir für $n = 3$ ein.

(IV)

In der Regel ein einfacher Satz, dass die Aussage gilt. Falls man die Induktionsvoraussetzung in der Klausur braucht, sollte man ihn auswendig kennen.

(IB)

Wir formulieren unsere Behauptung und schreiben einmal $A(n+1)$ auf.

(IS)

Die Prämisse von der wir starten ist $(n+1)^2$
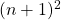
Ausmultiplizieren/1. Binomische Formel
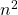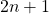$n^2$ mit $2n+1$ austauschen
Die Rechte Seite unserer Behauptung 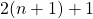$2(n+1) + 1$ , wenn wir diese umformen

wir setzen hier für $n^2$ unsere Induktionsvoraussetzung $2n+1$ ein. Denn wir haben bereits gezeigt, dass $n^2$ größer ist als $2n+1$ (Für alle $n \geq 3$ ) .
Wenn das stimmt und wir zeigen können, dass obwohl wir den kleineren Term für $n^2$ einsetzen, die Ungleichung immer noch wahr ist, dann muss auch unsere Induktionsbehauptung gelten.
Diese Methode wird bei allen – mir bekannten – Induktionsbeweisen von Ungleichungen verwendet.

An dieser Stelle könnten wir schon mit dem Beweis aufhören, denn wenn $n \geq 3$ ist, dann ist es klar, dass die linke Seite größer sein muss. Eine weitere Möglichkeit, es noch eindeutiger zu machen, ist es den Term so umzuformen, dass man es anhand der Struktur der Terme eindeutig erkennen kann(das ist aber oft gar nicht notwendig).

$2n + 1 +2n + 1 > 2n+3$
$2n +2n + 2 > 2n+2+1$
(zerlegen und umstellen)

Die beiden Terme der Ungleichung bestehen nun aus gleich vielen Gliedern an denen man eindeutig ablesen kann, das die Linke Seite größer sein muss als die Rechte.

Für einige kann die Darstellung oben im Rechenweg, etwas ungewöhnlich vorkommen, da sie es gewöhnt sind, Gleichungen bzw. Ungleichungen, beidseitig umzuformen. Wenn du das machen willst, kannst du das in dieser Form machen. Achte dabei aber darauf, das du die Folgepfeile korrekt anwendest:
(IS)
$(n+1)^2 >2(n+1) + 1$
$\Leftrightarrow \hspace{0.5cm} n^2 +2n + 1 > 2n + 3$
$\Leftrightarrow \hspace{0.5cm} 2n + 1 + 2n + 1 > 2n+3$
$\Leftrightarrow \hspace{0.5cm} 2n +2n + 2 > 2n+2+1$

Warum fügen wir die Voraussetzung ein?

Im Beispiel ersetze ich $n^2$ mit $2n+1$ , doch warum mache ich das? Der Grund ist dieser:
Du möchtest ja eindeutig zeigen, dass die linke Seite größer ist als die Rechte. Die Terme sind jedoch sehr unterschiedlich, die linke Seite $(n+1)^2$ ist ein Polynom vom Grad 2, während die Rechte ein Polynom vom Grad 1 ist. Außerdem haben sie unterschiedlich viele Glieder. Ihre Struktur unterscheidet sich, was es schwer macht direkt abzulesen, dass die linke Seite größer ist als die Rechte. In unserer Voraussetzung haben wir jedoch einen Term der unserer rechten Seite sehr ähnlich ist und zwar $2n+1$ . Da wir gezeigt haben, dass $n^2$ größer ist, können wir diesen ähnlichen Term nutzen, um unsere linke Seite in eine ähnliche Form zu bringen, wie die Rechte. Diese Methode verwenden wir in der Regel bei allen Arten von Induktionsbeweisen(zum Beispiel um das Summenzeichen mit einem Term zu ersetzen). Dafür nutzen wir immer die Aussage, welche wir im Induktionsanfang bewiesen haben.

Du verwendest die Induktionsvoraussetzung, um deinen Term im Induktionsschritt in eine passende Form zu bringen.

Zusammenfassung

Die ersten drei Schritte gleichen sich bei allen Induktionsbeweisen. Je nachdem was du beweisen willst, z.b Teilbarkeit, Ungleichungen, Summenformen, wirst du einen Unterschied beim Induktionsschritt haben. Bei Ungleichungen ist das Kernmerkmal, dass du zunächst zeigst, dass eine Ungleichung gültig ist und dann zeigst du mit Hilfe von Äquivalenzumformung, dass obwohl du einen Term verwendest der nicht gleich deines Ursprünglichen ist, die Ungleichung trotzdem noch wahr ist. Das geht am einfachste, indem du beide Seiten(bzw. den Vorhergehenden Term) in eine ähnliche Struktur bringst.

Übungen

Really nice: Aufgabensammlung zu Beweisen mit Vollständiger Induktion mit ausführlichen Lösungen

Hat dir der Inhalt gefallen?

Falls du mehr zu Themen der Informatik lesen willst, kannst du die Suche dafür verwenden:

Du bist der Meinung, das war der Beste Beitrag zum Thema Informatik den du jemals gelesen hast? Dann ist die einzig logische Schlussfolgerung, diesen Beitrag mit deinen Kommilitonen zu teilen. Oder auch nicht mach was du willst, ich bin nicht dein Dad.

Ungleichungen mit vollständiger Induktion beweisen für Noobs