Was du lernen wirst
In diesem Beitrag lernst du, wie man die Teilbarkeit mit Hilfe der vollständigen Induktion beweist.
Also Aussagen wie ![]() ist durch 2 teilbar. Dabei gehe ich davon aus, dass dir bereits die Grundlagen der vollständigen Induktion bekannt sind. Falls das nicht der Fall ist, kannst du diese in folgendem Beitrag auffrischen:
ist durch 2 teilbar. Dabei gehe ich davon aus, dass dir bereits die Grundlagen der vollständigen Induktion bekannt sind. Falls das nicht der Fall ist, kannst du diese in folgendem Beitrag auffrischen:
Was du mit damit anfangen kannst
Wenn du verstehst, wie man die Teilbarkeit mit Hilfe der vollständigen Induktion beweist, dann kannst du eine gute Note schreiben und es für den Rest deines Lebens wieder vergessen.
Es gibt bei allen Arten von Induktionsbeweisen(Ungleichungen, Teilbarkeit, Summenformen) ein Merkmal, was es unterscheidet. Auf dieses Merkmal weise ich immer in den Beiträgen hin! (siehe unten)
Wie beweist man die Teilbarkeit mit Hilfe der vollständigen Induktion?
Ich gehe davon aus, dass dir die Schritte der vollständigen Induktion bereits bekannt sind. Falls nicht, hier hast du eine kleine Zusammenfassung des Ablaufs:
- Induktionsanfang(Wir beweisen, dass die Aussage für die kleinste Zahl wahr ist.)
- Induktionsschritt(Wir beweisen, dass die Aussage auch für alle Zahlen über dem Startwert gilt.)
- Induktionsvoraussetzung formulieren(Wir schreiben aus, dass unsere Annahme für ein
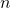 gültig ist.)
gültig ist.) - Induktionsbehauptung formulieren(Wir formulieren unser Ziel, und zwar, dass wenn es für ein beliebiges
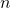 gilt, es auch für das darauf folgende
gilt, es auch für das darauf folgende 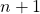 gilt.)
gilt.) - Beweis des Induktionsschrittes(Unter Verwendung der Annahme formen wir solange um, bis wir die Form der Behauptung erreichen.)
- Induktionsvoraussetzung formulieren(Wir schreiben aus, dass unsere Annahme für ein
Klausurtipp
Die ersten drei Schritte(Induktionsanfang, -voraussetzung, -behauptung) sind einfach, damit kannst du immer Punkte sammeln.
Ich werde das Konzept an einem einfachen Beispiel erklären und anschließend noch ein schwereres Beispiel zeigen:

Beweise mit Hilfe der vollständigen Induktion, dass folgende Aussage gilt.
![]() ist gerade
ist gerade ![]()
Kleine Randinformation: In dem Beweis, würdest du höchstens Abkürzungen wie (IA) = Induktionsanfang, (IV) = Induktionsvoraussetzung, (IB) = Induktionsbehauptung, (IS) = Induktionsschritt verwenden. Text gehört ebenfalls zur Beweisführung dazu.
Die Definition der Teilbarkeit lautet:
Eine ganze Zahl ![]() teilt eine ganze Zahl
teilt eine ganze Zahl ![]() genau dann, wenn es eine ganze Zahl
genau dann, wenn es eine ganze Zahl ![]() gibt, für die
gibt, für die ![]() gilt.
gilt.
(IA)
![]()
![]()
![]()
![]()
![]()
(IV)
Die Aussage ![]() gilt für ein beliebiges, aber festes
gilt für ein beliebiges, aber festes ![]() .
.![]()
(IB)
Wenn ![]() gilt, dann gilt auch
gilt, dann gilt auch ![]() .
.![]() ist gerade
ist gerade ![]()
(IS)
Quod erat demonstrandum.
(IA)
Da es nur für alle natürlichen Zahlen gelten soll, setzen wir für ![]() ein.
ein.
Je nachdem wie der Lehrer es definiert, kann es auch sein das die 0 enthalten sein muss. Dann würdet ihr hier für ![]() eine 0 einsetzen.
eine 0 einsetzen.
Der letzte Teil (![]() ) kommt dir womöglich unnötig vor, denn am vorhergehenden Schritt (
) kommt dir womöglich unnötig vor, denn am vorhergehenden Schritt (![]() ) kann man bereits erkennen, dass es durch 2 teilbar ist. Dennoch füge ich das hier hinzu, denn das Ausklammern des Teilers ist das Kernmerkmal beim Beweisen der Teilbarkeit, mit dieser Methode.
) kann man bereits erkennen, dass es durch 2 teilbar ist. Dennoch füge ich das hier hinzu, denn das Ausklammern des Teilers ist das Kernmerkmal beim Beweisen der Teilbarkeit, mit dieser Methode.
(IV)
In der Regel ein einfacher Satz, dass die Aussage gilt. Falls man die Induktionsvoraussetzung in der Klausur braucht, sollte man ihn auswendig kennen.
Die Darstellung ![]() sollte hier unbedingt stehen, da sie uns später von Nutzen sein wird.
sollte hier unbedingt stehen, da sie uns später von Nutzen sein wird.
(IB)
Wir formulieren unsere Behauptung und schreiben einmal ![]() auf. Dafür setzen wir für
auf. Dafür setzen wir für ![]() einfach
einfach ![]() ein.
ein.
(IS)
Das Ziel ist es ein Glied zu erzeugen, das so aussieht wie der Term in deiner Voraussetzung, hier ist das ![]() , damit wir ihn später ersetzen können.
, damit wir ihn später ersetzen können.
- Wir starten mit der Prämisse
 .
. - Dann lösen wir die Klammern auf, die Linke mit der 1. Binomischen Formel, die Rechte fällt einfach weg.
- Vereinfachen.
- Zerlegen von
 in
in 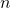 und
und  , warum siehst du im nächsten Schritt.
, warum siehst du im nächsten Schritt. - Jetzt kann ich
 klammern, weil es genau der Term aus der Voraussetzung ist, und ich weiß das dieser durch 2 teilbar is, daher kann ich ihn gleich mit
klammern, weil es genau der Term aus der Voraussetzung ist, und ich weiß das dieser durch 2 teilbar is, daher kann ich ihn gleich mit  ersetzen.
ersetzen. - ersetzen von
 mit
mit  .
. - Ausklammern unseres gesuchten Teilers(in diesem Fall die 2).
- Profit.
Bei dieser Methode ist das Ziel, irgendwo im Term den gleichen Term wie in der Voraussetzung zu bilden, sodass ich ihn mit der Darstellung der Teilbarkeit ersetzen kann.
Wie du dir den Term aus der Voraussetzung im Induktionsschritt baust, kommt auf die Aufgabe an. Manchmal kann es sein das du einfach ergänzen musst(also aus z.b ![]() einfach
einfach ![]() machst, weil du die Form
machst, weil du die Form ![]() mit deiner Darstellung der Teilbarkeit ersetzen willst. Dafür will ich dir folgendes Beispiel zeigen:
mit deiner Darstellung der Teilbarkeit ersetzen willst. Dafür will ich dir folgendes Beispiel zeigen:

Beweise mit Hilfe der vollständigen Induktion, dass folgende Aussage gilt.
![]() ist durch 5 teilbar
ist durch 5 teilbar ![]()
(IA)
![]()
![]()
![]()
![]()
![]()
(IV)
Die Aussage ![]() gilt für ein beliebiges, aber festes
gilt für ein beliebiges, aber festes ![]() .
.![]()
(IB)
Wenn ![]() gilt, dann gilt auch
gilt, dann gilt auch ![]() .
.![]() ist teilbar durch 5
ist teilbar durch 5 ![]()
(IS)
![]()
![]()
wir können ![]() auch als
auch als ![]() darstellen.
darstellen.![]()
hier ergänze ich die ![]() , um die gleiche Form zu erhalten wie in unserer Voraussetzung!
, um die gleiche Form zu erhalten wie in unserer Voraussetzung!![]()
jetzt ersetze ich die ![]() mit
mit ![]() , denn wir haben bereits gezeigt, das es durch 5 teilbar ist.
, denn wir haben bereits gezeigt, das es durch 5 teilbar ist.![]()
![]()
![]()
Gesuchten Teiler Ausklammern, um zu zeigen, dass es ein Teiler von dem Term in der Klammer ist!
Quod erat demonstrandum.
Sowas sehe ich gar nicht!!!
An einigen stellen des Induktionsschrittes hast du womöglich gedacht:
Sowas sehe ich nicht! Wie kommt man da drauf?
Someone on the Internet
Das ist vollkommen in Ordnung. Entspann dich einfach. Mach Übungen, schau dir die Lösungswege an. Nach einiger Zeit siehst du auch, wo du was ergänzen kannst, wo du klammern solltest, wo du eine Binomische Formel hast, oder faktorisieren musst. Alles eine Frage der Übung.
Zusammenfassung
Kurz gesagt, unterscheidet sich der Induktionsbeweis der Teilbarkeit nur im Induktionsschritt und der Voraussetzung. In der Voraussetzung macht es Sinn, die Teilbarkeit darzustellen ![]() . Dann müssen wir nur noch unseren Term umformen und uns den Term aus der Voraussetzung bilden, sodass wir ihn dann mit der Darstellung der Teilbarkeit ersetzen können. Anschließend wird der Teiler ausgeklammert, um eindeutig zu zeigen, dass der gesamte Term durch den Teiler in der Aussage teilbar ist.
. Dann müssen wir nur noch unseren Term umformen und uns den Term aus der Voraussetzung bilden, sodass wir ihn dann mit der Darstellung der Teilbarkeit ersetzen können. Anschließend wird der Teiler ausgeklammert, um eindeutig zu zeigen, dass der gesamte Term durch den Teiler in der Aussage teilbar ist.
Übungen
Hat dir der Inhalt gefallen?
Falls du mehr zu Themen der Informatik lesen willst, kannst du die Suche dafür verwenden:
Du bist der Meinung, das war der Beste Beitrag zum Thema Informatik den du jemals gelesen hast? Dann ist die einzig logische Schlussfolgerung, diesen Beitrag mit deinen Kommilitonen zu teilen. Oder auch nicht mach was du willst, ich bin nicht dein Dad.